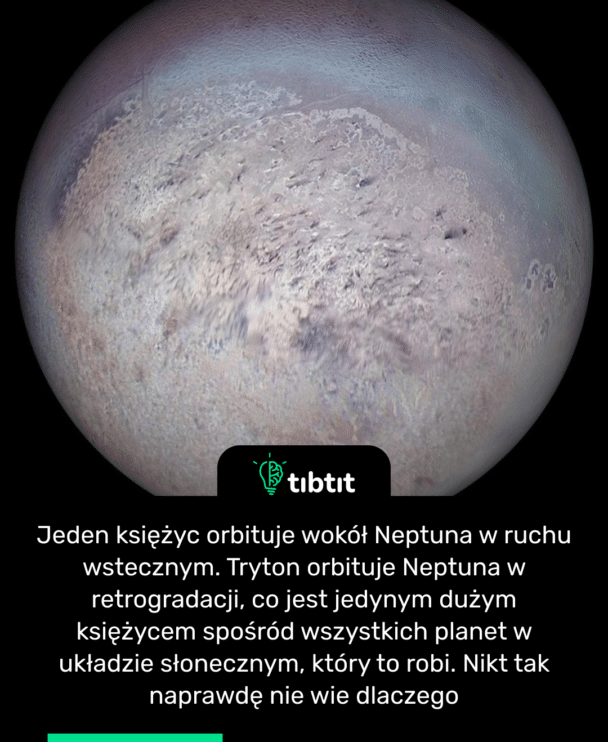
Czytaj więcej
Otaczający nas świat jest pełen tajemnic i niezwykle ciekawych historii, z których istnienia często zupełnie nie zdajemy sobie sprawy. Teraz jednak, dzięki TibTit.com masz do nich nieograniczony dostęp. W jednym miejscu gromadzimy najlepsze ciekawostki o świecie, które są zdumiewające, zabawne, a czasem też przerażające. Daj się zaskoczyć i codziennie odkrywaj nowe, fascynujące informacje na każdy temat!
Ciekawostki historyczne i interesujące fakty
Czy wiesz, że pierwszy odnotowany strajk robotniczy został zorganizowany przez budowniczych egipskich grobowców w 1170 r. p.n.e.? A zdawałeś sobie sprawę z tego, jak stresującym wydarzeniem dla pracowników NASA było pierwsze lądowanie na księżycu? Może o tym świadczyć między innymi fakt, iż przeciętnie wypalali oni aż 29 papierosów każdego dnia!
Te i inne interesujące ciekawostki z historii świata znajdziesz na stronie TibTit.com. Każdego dnia dostarczamy ci potężną dawkę wiedzy, której nie znajdziesz w szkolnych podręcznikach. Dzięki całej kategorii poświęconej tej tematyce poznasz nie tylko ważne, ale również zabawne fakty z historii, które mogą cię naprawdę zaskoczyć.
Ciekawostki naukowe, o astronomii i kosmosie, fizyce, biologii i chemii
Naukowcy nieustannie dostarczają nam coraz to nowszych wiadomości na temat otaczającego nas świata, ludzkiego ciała oraz umysłu. Nic więc dziwnego, że ciekawostki dotyczące nauki cieszą się tak dużym zainteresowaniem użytkowników serwisu TibTit.com. Można z nich wynieść nie tylko sporo ważnych informacji, ale też zapewnić sobie świetną rozrywkę.
Bo czy wiesz, że mapa języka z różnymi strefami smakowymi to zwykły mit? A może słyszałeś, że po 35. roku życia ludzki mózg zaczyna się powoli kurczyć? Okazuje się też, że warto oglądać horrory, jeśli planujesz się odchudzić! Podczas takiego 90-minutowego seansu można spalić nawet 113 kalorii. Jak więc widzisz, przeglądanie treści pojawiających się na TibTit.com może być niespodziewanie przydatne.
Ciekawostki ze świata natury, o zwierzętach i roślinach
Nasi użytkownicy wprost uwielbiają ciekawostki o zwierzętach, roślinach, zjawiskach atmosferycznych i szeroko pojętej naturze. Jest to przecież świat, który wciąż kryje przed nami mnóstwo tajemnic. Z pewnością mało kto wie, że na przykład według kryteriów botaniki truskawek i malin nie uznaje się za jagody, ale za to są nimi pomidory i banany.
Szczególnie duże zainteresowanie wzbudzają oczywiście nasze ciekawostki o psach i kotach, czyli o ukochanych pupilach ludzi. Czego więc dowiecie się na ich temat z TibTit.com? Na przykład tego, że to właśnie na psie przeprowadzono pierwszy zabieg wazektomii w 1823 r., a koty były popularnym prezentem ślubnym wśród Wikingów, gdyż były kojarzone z boginią szczęścia Freyą.
Ciekawostki o technologii, elektronice i multimedialne
Każdy postęp w technologii może realnie wpływać na poprawę jakości naszego życia. Warto więc trzymać rękę na pulsie i nieustannie poszerzać swoją wiedzę dotyczącą tej dziedziny. A pomóc ci w tym mogą informacje pojawiające się regularnie na TibTit.com. Czekają tu na ciebie wyjątkowo ciekawe dane, ale też zabawne fakty o technologii, które z pewnością przypadną ci do gustu.
Dzięki treściom udostępnianym w naszym serwisie dowiesz się na przykład, że satelity krążące wokół Ziemi są zaprojektowane w taki sposób, aby unikać zderzeń z meteorytami. Z kolei helikoptery skonstruowano tak, by mogły bezpiecznie lądować nawet po zgaśnięciu silnika. Ta kategoria tematyczna obejmuje też oczywiście ciekawostki internetowe, dotyczące na przykład pierwszego na świecie wirusa komputerowego, który powstał już w 1949 roku.
Ciekawostki lifestylowe, o aktorach, aktorkach i celebrytach
Chyba wszyscy doskonale wiedzą, czym jest kultura popularna i jak szerokie jest to pojęcie. Obejmuje ono między innymi tematy dotyczące filmu, muzyki, sztuki, książek, seriali, gier, komiksów, ale też celebrytów. Jeśli więc twoje zainteresowania mieszczą się w tych obszernych granicach, to z pewnością spodobają ci się treści pojawiające się na TibTit.com.
Z ciekawostek muzycznych można się na przykład dowiedzieć tego, że Elvis Presley nie napisał żadnej z ponad 600 nagranych przez siebie piosenek. Miłośników kinematografii na pewno zainteresuje z kolei fakt, że najdroższym wyprodukowanym do tej pory filmem są „Piraci z Karaibów: Na nieznanych wodach”. Takie ciekawostki filmowe to oczywiście tylko namiastka fascynujących informacji, które znajdziecie na TibTit.com.
Najbardziej zaskakujące i dziwne fakty
Typowe ciekawostki ze świata to dla ciebie za mało? TibTit.com przygotowało coś również dla użytkowników, którzy lubią poznawać naprawdę dziwaczne fakty dotyczące najróżniejszych dziedzin codziennego życia. Te dość niezwykłe, często śmieszne, ale też niepokojące dane to świetna podstawa do rozpoczęcia niejednej konwersacji.
Czego można się dowiedzieć, przeglądając kategorię WTF na TibTit.com? Na przykład tego, że w 2017 roku japońska policja przyjęła aż 10 tysięcy zgłoszeń dotyczących kradzieży bielizny. Albo też tego, że niemal połowa wszystkich urazów jąder wśród sportowców jest wynikiem gry w lacrosse. A to tylko początek, bo w naszym serwisie czeka na ciebie mnóstwo innych nietypowych ciekawostek tego rodzaju.
TibTit.com – wiedza i rozrywka
Nasz serwis jest prawdziwą kopalnią wiedzy w niestandardowym wydaniu. Krótkie informacje, które zaskakują i rozbudzają ciekawość czytelnika, są idealnym punktem wyjścia dla wielu interesujących dyskusji. Sprawdzaj codziennie, jakie ciekawostki przygotowaliśmy dla naszych użytkowników, komentuj i dziel się nimi z innymi.